Inhaltsverzeichnis
ENDOR
Die Elektron-Kern-Doppelresonanz (engl. electron nuclear double resonance, ENDOR) ist ein wichtiges Verfahren zur direkten Messung der Hyperfein-Wechselwirkung. Hierbei wird ein durch einen eingestrahlten Radiofrequenz-Puls erzeugter Kernspin-Übergang mithilfe der EPR detektiert.
Theorie
Häufig reicht die Auflösung von EPR-Spektren nicht dazu aus, alle relevanten Parameter des Spin-Hamiltons zu bestimmen und so ein möglichst umfassendes Bild über die Umgebung des Elektronenspins zu erhalten. Ein Hauptgrund dafür ist die große Anzahl von Übergängen in einem Spinsystem, in dem ein Elektronenspin mit mehreren Kernen koppelt. Diese Zahl der Übergänge wächst multiplikativ: Für n Kernspins mit den Spinquantenzahlen Ik ergibt sich die Zahl der erlaubten Elektronenspin-Übergänge ne zu
<latex>n_e=\prod_k^N(2I_k+1)</latex>
Geht man anstelle der Elektonenspin-Übergäge zur Betrachtung der Kernspin-Übergänge über, vereinfacht sich die Situation erheblich, da typischerweise jeder Kernspin mit nur einem Elektronenspin signifikant gekoppelt ist. Die Zahl der erlaubten Kernspin-Übergänge nn wächst nur noch additiv mit der Zahl der beobachteten Kernspins:
<latex>n_n=2(2S+1)\sum_{k=1}^nI_k</latex>
In Lösungen mittelt sich zudem noch die Kern-Quadrupolwechselwirkung heraus, so daß die Übergänge mI↔mI-1 mit verschiedenen mI entarten. Die Zahl der beobachteten Kernspin-Übergänge sinkt dann weiter auf:
<latex>n_n^{\rm liq}=n(2S+1)</latex>
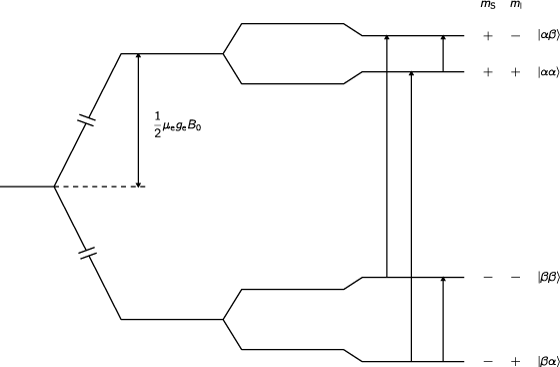
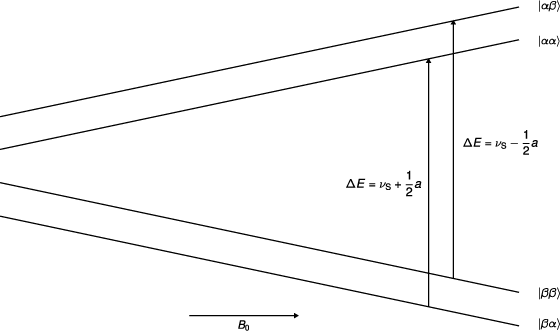
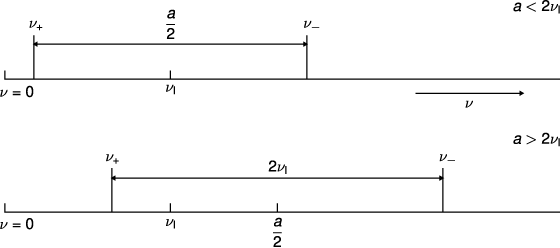
Vorteile von ENDOR
Die Zahl der Linien im Spektrum nimmt (abgesehen von zusätzlichen Quadrupolaufspaltungen für Kerne mit I≥1 im Festkörper) pro Satz äquivalenter Kerne um lediglich ein ENDOR-Linienpaar zu (Gesamtzahl: 2N). Die Liniendichte ist deshalb im ENDOR-Spektrum im allgemeinen um Größenordnungen geringer als im entsprechenden EPR-Spektrum.
gepulstes ENDOR
Literatur
Übersichtsartikel
- Arthur Schweiger: Pulsed Electron Spin Resonance Spectroscopy: Basic Principles, Techniques, and Examples of Applications, Angew. Chem. Int. Ed. Engl. 30 (1991) 265-292 online
- Claudius Gemperle and Arthur Schweiger: Pulsed Electron-Nuclear Double Resonance Methodology, Chem. Rev. 91 (1991) 1481-1505 online
